Los astrónomos usan medidas llamadas magnitudes para describir el brillo de un objeto en el cielo. Cuando los primeros astrónomos comenzaron a registrar las propiedades de las estrellas, no existía la tecnología para medir la cantidad de luz de forma precisa. Como resultado, los observadores desarrollaron el sistema de magnitudes, en el cual se compara el brillo de una estrella con respecto a otra. Cuando uno dice que una persona es dos veces más alta que otra, no se necesitan una unidad de medida. Similarmente, cuando medimos el brillo de una estrella en el cielo, no le anexamos una unidad de medida (como kilogramos, metros, o segundos) al final. La estrella brillante Vega, es comúnmente usada como al punto de comparación estándar, y el sistema está definido de forma que la magnitud aparente de Vega es aproximadamente cero.
Los astrónomos usualmente hacen referencia a dos tipos básicos de medidas de brillo:
Magnitud absoluta son usadas para cuantificar cuan brillante se vería un objeto si estuviera ubicado a una distancia estándar de 10 parsecs. Las magnitudes absolutas son particularmente útiles porque permiten comparar brillos reales e intrínsecos de diferentes objetos. El único problema es que la magnitud absoluta puede ser difícil de determinar, porque requiere conocer la distancia de un objeto a la Tierra.
Absolute magnitude is used to quantify how bright an object would appear if it were at a standard distance of 10 parsecs away. Absolute magnitude measurements are particularly useful because they allow us to compare the true, intrinsic brightness of different objects. The only problem is, absolute magnitudes can be difficult to determine, because they require knowing an object’s distance from the Earth.
Por simpleza, vamos a usar magnitudes aparentes para la mayoría de las actividades de Voyages – sólo recuerda que esta medida no entrega la verdadera luminosidad de un objeto, solo cuan brillante se ve desde nuestra ubicación.
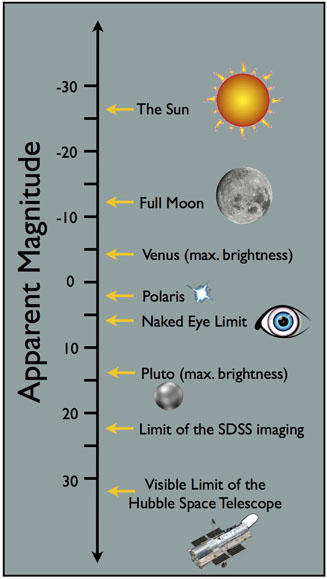
Por razones históricas, los objetos del cielo (cómo la mayoría de las estrellas) que se ven más débiles que la estrella Vega, tienen magnitudes aparentes positivas; mientras que objetos en el cielo (como la luna llena) que se ven más brillantes que Vega, tienen magnitudes aparentes negativas. En el caso de la luna llena, la magnitud aparente es -13. ¡El Sol tiene una gigante de -27! Venus, que usualmente puede verse incluso incluso durante el día, es bastante brillante, con una magnitud aparente de -5. Pero Plutón, que no se puede ver sin un telescopio, tiene una magnitud de 14.
Entonces, la escala de magnitud corre en dirección opuesta a lo que uno esperaría…mientras más alta la magnitud, mas débil se ve el objeto! Piensa en la escala de magnitud como una carrera donde los ganadores llegan primero. Es más fácil pensar en la estrella más brillante en una carrera de brillo en primer lugar y los objetos más débiles en el 4.º, 5.º, o incluso 23.º lugar.

El catálogo SDSS guarda cinco magnitudes distintas para cada objeto. Para comprender esto de manera más sencilla, imagina que el telescopio de SDSS tiene cinco pares de gafas con vidrios de distintos colores que se puede poner antes de mirar al cielo. Estas “gafas” se conocen como filtros. Las estrellas y galaxias tienen magnitudes ligeramente diferentes dependiendo del filtro con el que se observen. SDSS mide magnitudes para estos cinco filtros. Si quieres saber más sobre ellos, por favor visita nuestra pagina de Filtros de la sección de Pre-vuelo.
Para nuestras actividades de Voyages te recomendamos que elijas la magnitud de un filtro para medir el brillo de una estrella y que te mantengas con esa elección durante toda la actividad.
Calculando magnitudes aparentes
Probablemente te estas preguntando que nos dice exactamente exactamente la magnitud aparente, acerca del brillo relativo de diferentes objetos. Las magnitudes está construida en base a una escala logarítmica, que nos permite comparar objetos con brillos radicalmente diferentes sin tener que usar números increíblemente grandes. La escala de magnitudes funciona de manera que el incremento de 1 en magnitud corresponde a una disminución del brillo en un factor de aproximadamente 2.5. En otras palabras, un objeto con una magnitud de 5 es 2.5 veces menos brillante que uno de magnitud 4.
La propiedad física que la magnitud aparente mide es el flujo, que corresponde a la cantidad de luz que llega a la tierra sobre un área determinada, en una cierta cantidad de tiempo. Abreviado como f, el flujo, se relaciona con las magnitudes del SDSS, m, de la siguiente forma:
m = 22.5 – 2.5 x log10(f)
El punto cero de esta escala (el punto relativo con respecto el cual los otros brillos son comparados) es el flujo de una fuente estándar, que tiene una magnitud definida como 22.5.
Una variación de la ecuación de arriba, puede ser usada para relacionar la diferencia entre las magnitudes de dos objetos (m1 y m2) con el cuociente de sus flujos, f1/f2:
m1 – m2 = -2.5 x log10 (f1/f2)
El sol, que es 14 unidades de magnitud aparente más brillante que la luna, es casi 400.000 veces más brillante si uno compara las intensidades de su luz directamente (esto probablemente no es sorprendente porque podemos ver de forma segura la luna llena pero no el Sol). Entonces ahora puedes valorar como las magnitudes nos ayudan a comparar objetos del cielo con brillos extremadamente diferentes, sin tener que usar números enormes.
Relacionando magnitudes aparentes y absolutas
Como ya vimos, el brillo aparente de un objeto depende de su distancia a nosotros. Mientras más se aleja un objeto brillante, se ve menos brillante. Por tanto, si queremos saber que tan brillante es realmente un objeto, necesitamos saber su distancia.
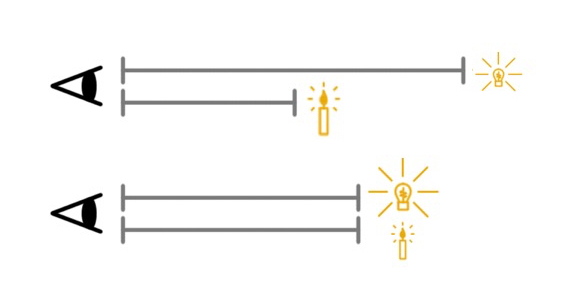
Imagina una bombilla de luz que tiene mayor luminosidad que una vela, lo que significa que emite más luz por segundo que la vela. La bombilla se verá más brillante que la vela si ambas se encuentran a la misma distancia del observador; pero la vela y la bombilla pueden tener el mismo brillo aparente si la bombilla está mucho más lejos.
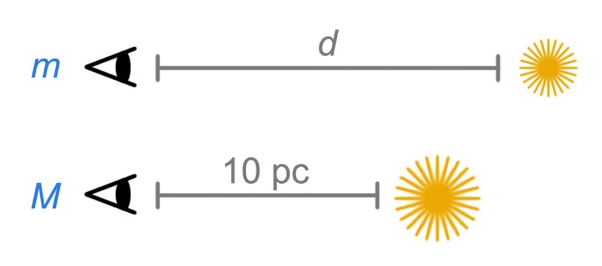
La magnitud aparente, m, mide que tan brillante se ve un objeto, dada su distancia a la tierra
La magnitud absoluta, M, mide que tan brillante se vería un objeto si estuviera exactamente a 10 parsecs de distancia.
Distancia, magnitud aparente, y magnitud absoluta, están relacionadas por la ecuación del módulo de distancia:
m – M = 5 log10(d) – 5
donde M representa la magnitud absoluta, m representa la magnitud aparente, y d es la distancia al objeto en parsecs. Finalmente, la base del logaritmo es 10.
