Understanding Coordinates on the Celestial Sphere
If you want to go someplace in a car, it is handy to have a map or a GPS system to assist you. The same is true when you drive a telescope to a position on the sky. Astronomers refer to this as slewing the telescope, and to do so you need to provide the location of your target. Astronomers use a coordinate system similar to latitude and longitude to define the location of any object in the celestial sphere. Here’s how it works:
Reference Lines in the Sky
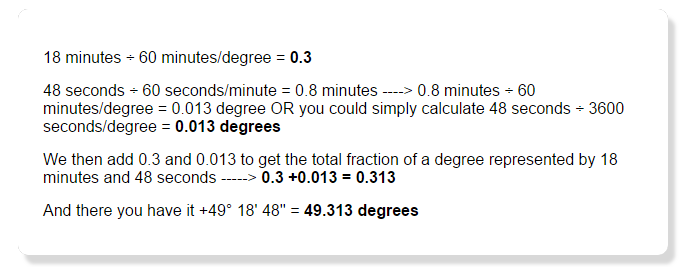
Imagine a giant light bulb at the center of a transparent Earth that projects the lines of longitude and latitude onto the night sky. You now have a grid on the sky that you can use to define the location of any object. Astronomers give these projected lines unique names. Lines of longitude are now called right ascension (RA) and the lines of latitude are called declination (Dec). Because lines of right ascension appear to cross the sky from east to west in time with the rotation of the earth, they are measured in divisions of hours, minutes, and seconds. There are 24 hours in a day, so there are 24 hours of right ascension on the sphere of the sky. Likewise, each hour is divided into 60 minutes of RA, and each minute is divided still further into 60 seconds.
Declination is a much easier measurement to visualize since the distance between these lines remains uniform as you move north and south across the sky. We measure lines of declination using degrees, minutes, and seconds as we would most curved surfaces. The equator projected onto the night sky is referred to as the celestial equator and given the declination of zero degrees. All lines of declination north of the celestial equator are positive measurements from zero at the equator to +90 at the celestial north pole. Lines of declination south of the celestial equator are negative measurements from zero to -90 at the celestial south pole.
Recording the locations of objects in the sky
The Sloan Digital Sky Survey (SDSS) stores hundreds of pieces of information about more than four million objects in organized collections of tables in the SDSS database. The database is stored and accessed by computers. When programming computers to search and retrieve information, it is not convenient to have one measurement contain multiple units such as we find in traditional RA and Dec measurements. It is for this reason that RA and Dec measurement are reported in the SDSS as decimal degrees. Let’s see how this works.
Converting to Degree Measurements for RA and Dec
Calculating the degree measurements for RA and Dec can be confusing; because Dec formulas are less complicated, however, let’s start with them first.
For Example:
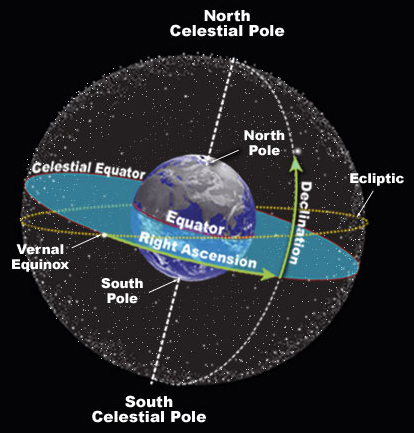
The star Alkaid, the last star in the handle of the Big Dipper, has a declination of +49° 18′ 48” (49 degrees 18 minutes and 48 seconds) Since there are 60 arc minutes in a degree and 60 arc seconds in one arc minute, we simply divide:
Right ascension is a bit more complex to understand and complicated to calculate. Remember that we measure right ascension in units of time. This is very handy because lines of right ascension are further apart at the celestial equator than they are at the poles, but the amount of time needed for the sky to rotate overhead from one point to the next is constant. Because we divide circles into 360 degrees and there are 24 hours in a day, we know that 360 / 24 (or 15 degrees) of the sky dome will rotate past an observer in one hour.
Once you understand the relationship between hours and degrees (or time and distance), the rest is almost easy:
The star Alkaid has a right ascension of 13h 47min 32sec. Fifteen degrees of sky pass overhead for each hour of right ascension (15 x n hours = degrees). If 15 degrees of sky pass overhead in one hour and there are 60 min of time in each hour then 60/15 = 4 represents the number of minutes needed for 1 degree to pass overhead. By the same reasoning it takes 240 seconds (3600/15) for each degree to rotate past the observer on the ground. When we put this together the conversion from Hours, Minutes, Seconds to degrees looks like this:
You can see how decimal degrees are simpler numbers to work with when storing information and programming. So remember, whenever you are searching the SDSS database for objects or pointing one of the SkyServer tools to a different part of the sky, the location information will be displayed in decimal degrees.